CHE204B Physical & Quantum Chemistry

Question 1

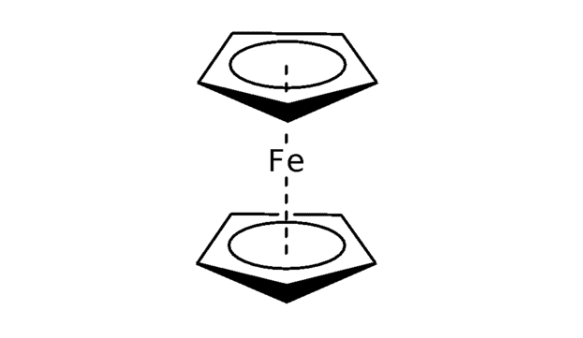
(a) List all the symmetry elements of a FeCp2 molecule in an eclipsed conformation shown below and identify the symmetry point group to which it belongs[4 marks]

(b) What is the highest possible degeneracy of a vibration of a Cr(CO)6 molecule? Explain your answer. [2 marks]

(c) Consider a trigonal bipyramidal molecule Fe(CO)5.

(i) To which point group does this molecule belong? [2 marks]

(ii) How many normal modes and how many CO stretching vibrations belong this molecule possesses? [2 marks]

(iii) Determine the irreducible representations of CO stretching vibrations of a Fe(CO)5 molecule. Clearly show all your work. [6 marks]

(iv) Which of the stretching vibrations of a Fe(CO)5 molecule are active in IR and which in Raman spectra? Justify your choice. [4 marks]

Question 2

(a) Derive the ground-state term symbols for the following atoms or ions:

(i) Fluoride, F – [2 marks]

(ii) Arsenic, As [2 marks]

(iii) Scandium ion, Sc2+ [2 marks]

(b) What values of J are consistent with the terms 2P and 3D? How many states with different values of MJ correspond to each? [4 marks]

(c) Consider the emission spectrum of the alkaline earth element Ca exhibiting two emission lines at λ1 and λ2 that originate from the 2P excited state (spin-orbit split). Derive an expression to compute the value of the spin-orbit coupling constant. [6 marks]

(d) Identify the symmetry species of the Symmetry Adapted Linear Combination (SALC) 𝜙 = 𝜓𝑂 ′ − 𝜓𝑂 ′′ in the C2v molecule NO2, where 𝜓𝑂 ′ is a 2px orbital on one O atom and 𝜓𝑂 ′′ is a 2px orbital on the other O atom. [4 marks]

Question 3

Answer all parts.

(a) Determine the symmetry point groups of the mer- and fac- isomers of the complex [Re(CO)3(NCMe)3] and deduce the irreducible symmetry representations generated by the three stretching vibrations of the CN ligands in each of the isomers. [Regard NCMe as a linear ligand.] [10 marks]

(b) For each isomer discussed in part (a), state with reasoning which vibrations are IR active, and which are Raman active and how many bands will be observable in IR and Raman spectra. How can you distinguish the two isomers using their vibrational spectra? [5 marks]

(c) Determine the results of the following multiplications of symmetry operations for the anthracene molecule (chemical structure shown below, C2 represents the main axis). [5 marks]

Question 4 Answer all parts.

(a) Demonstrate that the linear combination 𝐴̂ − 𝑖𝐵̂ is not Hermitian if 𝐴̂ and 𝐵̂ are Hermitian operators. [3 marks]

(b) Show if the operators 𝑝̂𝑥 2 and 𝑝̂𝑦 2 commute. [3 marks]

(c) Consider the functions ℎ1 = 𝑠 − 𝑝𝑥 + 𝑝𝑦 − 𝑝𝑧 and ℎ2 = 𝑠 + 𝑝𝑥 − 𝑝𝑦 − 𝑝𝑧. Determine the value of the integral ∫ ℎ1ℎ2𝑑𝜏. Justify your answer. [4 marks]

(d) Decompose the representation below into the irreducible representations of C3v. Justify your answer. [4 marks]

(e) Describe the symmetry-adapted core and valence orbitals of H2O in the C2v point group. [3 marks]

(f) Consider the 3𝑑𝑦𝑧 orbital of the central atom of a molecule with symmetry C2v. Which symmetry representation does 3𝑑𝑦𝑧 belong to? Justify graphically your answer. [3 marks]