CEGE0040 - Structural Dynamics

Question 1

A frame consists of two steel columns (E = 210 GPa) and a top beam that is connected to an adjacent wall by means of an axial spring of stiffness k (see Figure Q1a). The columns are 3 m high and are inextensible and light so that the mass of the frame, m=1.6 tonne, can be considered concentrated in the rigid top beam. The second moment of area I = 264 cm4 is the same for the two columns. All connections are moment-resisting.

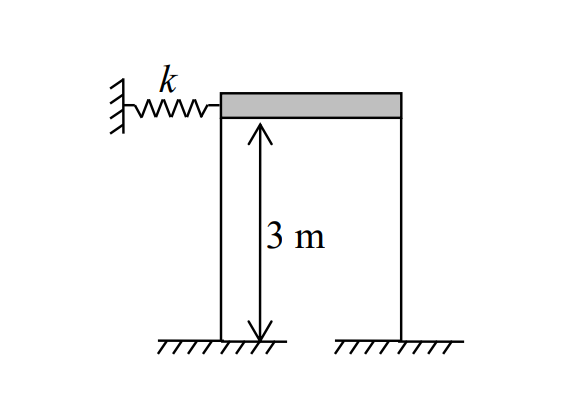
(a) If the sway natural frequency of in-plane vibrations of the system is 1.5 Hz, deduce the value of k. [8 marks]

(b) A resonance test was carried out on the structure by applying a sinusoidal lateral force to the frame over a range of frequencies and measuring the resulting displacement. The results are plotted in Figure Q1b, which shows the dynamic magnification factor against the normalised frequency. Using the half-power bandwidth method, estimate the damping factor for this system. [4 marks]

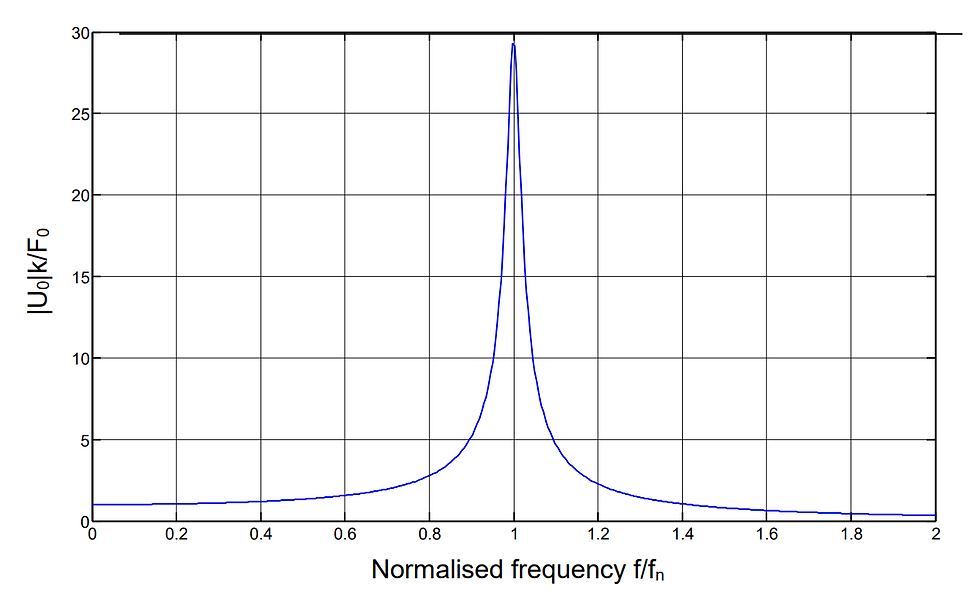
(c) The system is now subjected to a sinusoidal excitation with frequency f = 1.2 Hz and force amplitude F0 =1 kN. What is the steady-state amplitude of the response of the structure to this excitation? [5 marks]

(d) The distance between the unstressed frame and the fixed wall to its left is 35 mm. What range of forcing frequencies would cause the frame in its steady-state response to hit the wall for force amplitudes larger than 1 kN? [8 marks]

Question 2

Figure Q2 shows the simplified elevation of a frame structure with a mezzanine floor halfway up the height of the building. The mezzanine slab has the same mass as the roof slab (top). The structure is supported by columns of stiffness as indicated in the figure. Assume that the horizontal slabs are rigid and the axial deformations in the columns are negligible. Ignore any damping.

(a) Write down the governing differential equation of motion for this system for the case that a lateral force p(t) acts on the roof of the structure as shown in Figure Q2. [5 marks]

(b) Determine the natural frequencies and the corresponding mode shapes. Sketch the mode shapes. [9 marks]

(c) The lateral point load p, applied to the roof of the structure, is ramped up quasistatically from zero amplitude until the lateral displacement of the roof with respect to the ground is one unit of length. Explain the significance of the word ‘quasistatic’ in this process and deduce the corresponding displacement of the mezzanine floor. [5 marks]

(d) The structure is then released from the final state reached in (c) and allowed to vibrate freely. Find the expression for the displacements of the two masses in the subsequent motion. [6 marks]

Question 3

The three-storey shear frame shown in Figure Q3(a) has the structural characteristics as indicated in the figure, with 𝐸𝐼 = 20 MNm2 and m0 = 20 tonnes. Figure Q3 shows the acceleration response spectrum of a single degree of freedom system to the Taiwan 1986 ground motion.

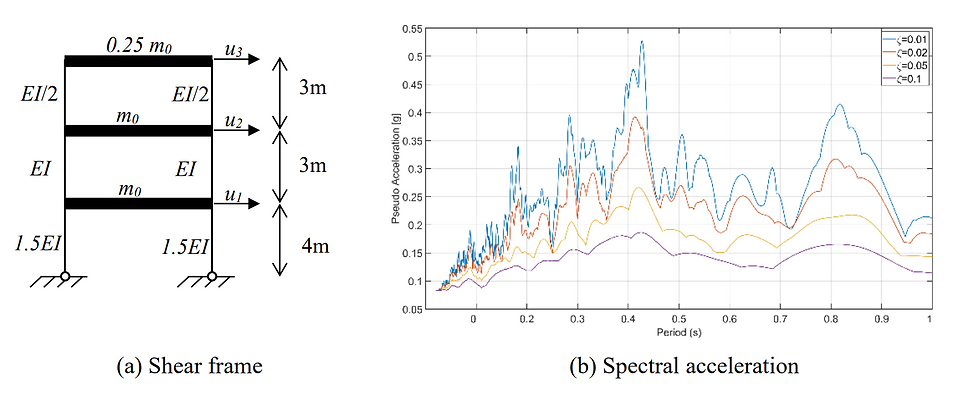
(a) Determine the mass and stiffness matrices for the frame. Calculate their coefficients numerically. [4 marks]

The natural periods of this frame are 0.82 s, 0.17 s and 0.12 s

(b) Calculate the first natural frequency and the two effective modal masses. What can you deduce in terms of modal contribution to the overall response? [10 marks]

(c) Explain the key limitations of modal combination rules. [3 marks]

(d) Using Figure Q3(b), estimate the total base shear demand on this frame from the Taiwan 1986 ground motion, assuming 2.5 % modal damping. [3 marks]

(e) Estimate the inter-storey drift and the moment demands on the ground floor and first-floor columns. [5 marks]

Question 4

(a) (i) Describe what numerical damping is and explain its particular significance in the context of direct integration for structural dynamics.

(ii) Describe the main types of nonlinear analyses in the context of earthquake engineering and briefly discuss their pros and cons. [6 marks]

(b) Derive the recurrence relationship that follows from discretising the equation of motion for a damped single degree of freedom dynamical system using Euler’s backward scheme. Initialise the first two displacement samples using initial rest conditions. [4 marks]

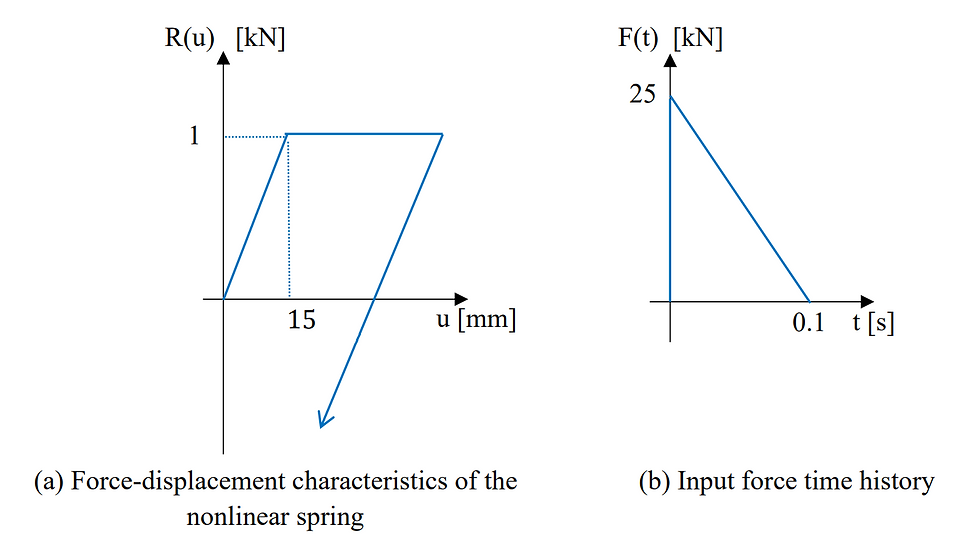
(c) A single degree of freedom system is made of a mass 𝑚0 = 60 tonnes, and the elastoplastic spring defined by the force-displacement relationship shown in Figure Q4(a). The mass is subjected to the force defined by the time history shown in Figure Q4(b). Ignore any viscous damping and assume the system is initially at rest.

(i) Compare the elastic period to the duration of the impulsive force. How do you expect the system to respond initially? [3 marks]

(ii) Taking a time step Δ𝑡 = 0.02 s, calculate the displacement of the system for the first 10 time steps. [10 marks]

(iii) Calculate the energy dissipated during this 0.2 s time interval. [2 marks]