5SSPP213 Econometrics
- 2695389849
- Aug 31, 2021
- 4 min read
SECTION A: 25 MARKS IN TOTAL
Answer the following questions or in case of a statement, state whether the following statements are correct and give a reason for your answer.
i Which of the following assumptions must hold to create a confidence interval on the difference between two groups’ means?
(a) At least 2% of the population is sampled
(b) The observations are independently sampled
(c) The variance of group 1 is the same as the variance of group 2
(d) The populations are normally distributed
(e) The model is linear in parameter (f) The expected value of the error term is zero
ii As many infectious diseases, the cumulative number of Covid-19 cases over time (t) has been modelled as an exponential function: cases(t) = α0e α1t . How would you estimate the parameters α0 and α1 using OLS?
iii What is the relationship between the sample size and the t-test?
iv A researcher would like to test whether a new teaching method increases the average grades in econometrics by a minimum of x points compared to the national average of 60, where x is the last digit of your student card number. The standard deviation of the national average is 10 and it is expected to be unaffected by the new teaching method. The researcher is planning to use a one sample (one sided) t-test to test the differences between the grade distribution of the cohort taught with the new method and the national average at the 1% statistical significance level. The researcher has a sample of 100 subjects. What is the statistical power of the test? Use the statistical tables provided.
v In a model estimating the monetary returns to education, the variable IQ score can be a suitable instrumental variable for education.

SECTION B: 20 MARKS IN TOTAL
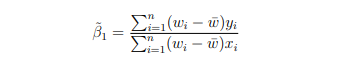
i Show that the estimator above is unbiased.
ii How would you calculate the variance of the estimator?
iii Would you expect the variance of the estimator to be smaller or larger than the variance of the OLS estimator? Use your intuition.
SECTION C: 25 MARKS IN TOTAL
A researcher wants to evaluate an educational intervention that changes teaching practices in schools from conventional lecture-oriented classes to “work in group” classes where students are encouraged to work in groups and do projects together. The programme is implemented in selected classrooms within schools. The outcome of interest is cooperative behaviour in a team task outside the class.
where Yicst indicates the outcome of interest for student i in classroom c of school s at time t. GLPcst represents a dummy variable indicating whether the Group Learning Programme was in operation in classroom c in school s at time t. Xicst is a vector of individual characteristics of students measured at baseline and includes sex, whether parents are separated, mother age, mother education, number of siblings and religion. γcs represents classroom-within-school fixed effects and ηt represents time fixed effects. The researcher has baseline and endline data.
i What does the coefficient γcs capture? Make an example.
ii Which difference does the coefficient β1 capture?
iii Someone suggests that the number of siblings has a non-linear quadratic effect on the outcome. How would you adjust the model to test for this possibility? How would you decide if this suggestion is relevant and the model should include a non-linear effect in the number of siblings?
iv Someone criticises the model by saying that teacher’s sex is an omitted variable. Under which conditions would teacher’s sex create an omitted variable bias on the coefficient of GLP? Would the bias be positive or negative?
v The researcher decides to cluster the standard errors at the classroom level. What does that mean and is it appropriate in this case?
SECTION D: 30 MARKS IN TOTAL
Two researchers are interested in understanding the impact of an anti-anxiety training on student exam performance. They set up a Randomized Control Trial by which students who volunteered to take part into the study are randomly assigned to the training (treatment group) or to a control group with no training. The researchers collect data before the anti-anxiety training (pre-treatment) and after the anti-anxiety training (post-treatment). They use a variety of models to estimate the effect of the training on student performance in a logic test, measured by the number of correct answers in the test.
The subscript pre on any variable indicates that the variable’s measurement is collected before the treatment; the subscript post indicates that the variable’s measurement is collected after the treatment.
Column (1) presents the estimates of a model in which the dependent variable is the measurement post-treatment. Column (2) and column (3) present the estimates of models in which the dependent variable is the change between the measurements pre- and post-treatment: ypost − ypre.
i Is the parameter δ an estimate of the Average Treatment Effect (ATE) or the Average Treatment effect on the Treated (ATT)? What is the difference?
ii Column (1) and column (2) yield exactly the same estimates except for the coefficient β1. This is because the model in column (2) is a re-parameterization of the model in column (1). Show how one could reparameterize the model in column (1) to get the model in column (2).
iii Does the estimated effect of Training in the model in column (2) differ statistically from the effect estimated in the model in column (3)?
iv Test the hypothesis that the estimated effect of Training in the model in column (3) is equal to 1.5 at the 1% significance level. Use the statistical tables provided.
v How would you modify the model to test that the quadratic effect of trait anxiety differs between men and women?



Comments